プッシュダウンオートマトンについて
プッシュダウンオートマトンについての個人的なまとめです。PDA の例を挙げるのに 「アンダースタンディングコンピュテーション」 の内容を参考にしています。
プッシュダウンオートマトン (PushDown Automaton, PDA)
プッシュダウンオートマトン (PDA) は内部状態として任意容量のスタックを持つ 有限状態機械 (FSM) である。FSM 同様、遷移規則に基づいて入力文字列が受理可能かを判断する。PDA が FSM と異なるのは以下の2点である。
- 各遷移時にスタックと文字のやり取り (push, pop) を行うことが許されている
- 遷移規則が現在の状態、入力文字、次の状態、pop される文字、push する文字から構成される
PDA の例
’(())’ のように開き、閉じ括弧が一致した文字列を受理する PDA は以下のように表現できる。全体的な見方は FSM のときに使用したものと同じである。遷移規則は <入力文字>, <pop される文字>/<push される文字> を付記した状態間の矢印で表している。計算中スタックが空であることを判断するためにスタックの底を表す文字として ‘$’ を使用している。
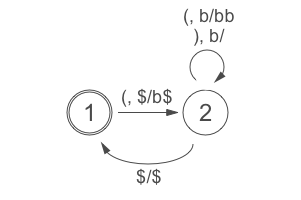
この PDA をシンプルにプログラムで実装すると以下のようになる。
from collections import namedtuple
class PDARule(namedtuple('PDARule', ['start_state', 'character', 'next_state', 'popped_char', 'pushed_chars'])):
'''
Transition rule of pushdown automaton.
This class is immutable.
'''
__slots__ = ()
def is_applied_to(self, char, state, stack):
'''
Return True if this rule can be applied to the passed condition of PDA.
'''
if char is not None:
return char == self.character and \
state == self.start_state and \
stack[-1] == self.popped_char
else:
return self.character is None and \
state == self.start_state and \
stack[-1] == self.popped_char
def apply(self, char, state, stack):
'''
Apply this rule and calculate a next state and stack.
'''
if not self.is_applied_to(char, state, stack):
raise RuntimeError('cannot apply the rule: %s' % (str(self)))
next_state = self.next_state
next_stack = list(stack)
next_stack.pop()
next_stack += reversed(self.pushed_chars)
return (next_state, next_stack)
class DPDA:
'''
Simulator of deterministic pushdown automaton.
'''
def __init__(self, initial_state, rules, accept_states):
self.initial_state = initial_state
self.rules = rules
self.accept_states = accept_states
def does_accept(self, string):
'''
Return True if a passed string is in the language of this automaton.
'''
state = self.initial_state
index = 0
stack = ['$'] # '$' means the bottom of stack
while index < len(string):
if not self.has_available_rules(string[index], state, stack):
return False
state, stack = self.transit(string[index], state, stack)
index += 1
return state in self.accept_states
def collect_available_rules(self, char, state, stack):
return [ rule for rule in self.rules if rule.is_applied_to(char, state, stack) ]
def has_available_rules(self, char, state, stack):
return len(self.collect_available_rules(char, state, stack)) > 0
def transit(self, char, state, stack):
available_rules = self.collect_available_rules(char, state, stack)
if len(available_rules) == 0:
raise RuntimeError('cannot transit since this DPDA is in the stuck state')
# apply a rule (this is deterministic, so there should be only one available rule)
rule = available_rules[0]
next_state, next_stack = rule.apply(char, state, stack)
# epsilon moving if necessary, which consumes no input.
if self.has_available_rules(None, next_state, next_stack):
return self.transit(None, next_state, next_stack)
else:
return (next_state, next_stack)
if __name__ == '__main__':
# Transition rules to accept strings consisting of correct pairs of '(' and ')'.
transition_rules = (
PDARule(1, '(' , 2, '$', ['b', '$']),
PDARule(2, '(' , 2, 'b', ['b', 'b']),
PDARule(2, ')' , 2, 'b', []),
PDARule(2, None, 1, '$', ['$']),
)
# Simulator of DPDA
dpda = DPDA(1, transition_rules, {1})
assert dpda.does_accept('') == True
assert dpda.does_accept('(())') == True
assert dpda.does_accept('(()())') == True
assert dpda.does_accept('(()') == False
assert dpda.does_accept('(()))') == False
決定性と非決定性
FSM 同様、常に適用できる遷移規則が 0 または 1 つに定まるならば、その PDA は決定性を持つ。これを決定性プッシュダウンオートマトン (Deterministic Pushdown Automaton, DPDA) と呼ぶ。
決定性を持たない場合、換言すれば適用可能な遷移規則が複数存在することを許す場合、これを非決定性プッシュダウンオートマトン (Nondeterministic Pushdown Automaton, NPDA) と呼ぶ。
FSM では決定性の有無で計算能力に差異は無かったが、PDA では NPDA の方がより高い計算能力を持つ。例えば DPDA では受理できず、 NPDA で受理できる以下のような言語が存在する。
e.g. 文字 ‘a’, ‘b’ で構成される文字列長が偶数の回文を受理する NPDA
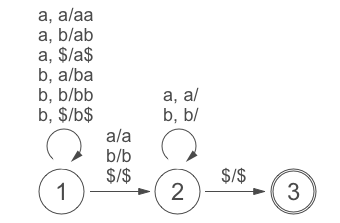
ちなみに任意の文字列長を受理する NPDA を作成する場合、例えばもう一つ状態を増やし、そこで読込文字を消費させるような動きをさせればよい。
計算可能なこと
各 PDA は文脈自由文法を表現しており、入力文字列がその言語の要素であるかを計算する。逆も成立し、任意の文脈自由言語に対してそれを受理する PDA が存在する。
正規言語は文脈自由言語の部分集合であり、 任意の FSM と等価な PDA が存在する。
計算不可能なこと
FSM と同様で、文脈自由文法を認識する以上のことは不可能。