有限状態機械についての個人的なまとめです。

有限状態機械 (Finite State Machine, FSM)

計算論の分野における有限状態機械 (FSM) とは抽象機械で表される計算モデルの一種である。FSM は入力された文字列が自身の定義する文法で受理可能かを判断する。FSM は内部状態として現在の状態を持ち、これと一連の遷移規則から構成される。ここでの遷移規則とは現在の状態と入力文字から次の状態を決定する規則である。FSM が遷移可能な状態数は有限であり、遷移規則の数も有限である。

換言すれば、文字列が FSM に受理されるとは、入力を一文字ずつ読み込み、開始状態から遷移規則に基づいて終了状態まで遷移できるということである。

有限状態機械を有限オートマトンと呼ぶこともある。

FSM の例

‘ab’ で始まる文字列のみを受理する FSM は以下のような図で表現される。図中の数字付きの円が状態、文字付きの矢印が遷移規則を表す。開始状態は 1 、終了状態は二重円で表されるとする。

deterministic finite automaton

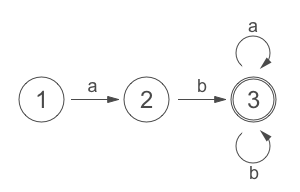
上記 FSM の動作をプログラムでシンプルに実装すると以下のようになる。

from collections import namedtuple

class FSMRule(namedtuple('FSMRule', ['start_state', 'character', 'next_state'])):
    '''
    Immutable class representing transition rules.
    '''
    __slots__ = ()


class DFA:
    '''
    Simulator of deterministic finite automatons.
    '''
    def __init__(self, initial_state, rules, accept_states):
        self.initial_state = initial_state
        self.rules = rules
        self.accept_states = accept_states

    def does_accept(self, string):
        '''
        Return true if a passed string is in the language of this automaton.
        '''
        state = self.initial_state
        index = 0
        while index < len(string):
            if not self.does_accept_char(string[index], state):
                return False
            state = self.transit(string[index], state)
            index += 1
        return state in self.accept_states

    def does_accept_char(self, char, state):
        return any(map( \
            lambda rule: rule.start_state == state and rule.character == char, \
            self.rules))

    def transit(self, char, state):
        accepted_rules = list(filter( \
            lambda rule: rule.start_state == state and rule.character == char, \
            self.rules))
        if len(accepted_rules) == 0:
            return None
        return accepted_rules[0].next_state

if __name__ == '__main__':
    # Transition rules to accept strings starting with 'ab'.
    # FSMRule(start_state, character, next_state)
    transition_rules = (
            FSMRule(1, 'a', 2), 
            FSMRule(2, 'b', 3),
            FSMRule(3, 'a', 3),
            FSMRule(3, 'b', 3),
            )
    dfa = DFA(1, transition_rules, {3})
    assert dfa.does_accept('ab') == True
    assert dfa.does_accept('ababaab') == True
    assert dfa.does_accept('a') == False
    assert dfa.does_accept('b') == False

決定性と非決定性

有限状態機械には決定性のものと非決定性のものが存在する。

上記例では現在の状態と読込文字が決まれば、適用可能な遷移規則は 0 または 1 つに定まる。このように遷移の道筋が一通りに決まる場合、これを決定性有限オートマトン (Deterministic Finite Automaton, DFA) と呼ぶ。

有限状態機械に以下の拡張を加えたものは非決定性有限オートマトン (Nondeterministic Finite Automaton, NFA) と呼ばれる。NFA では適用可能な遷移規則が複数存在し得る。

  • 同一の内部状態、入力文字から異なる状態への遷移
    • 上記例でいえば、1 から 1 への ‘a’ 遷移を加えたようなケース
      • ‘ab’ を含む文字列が受理されるようになる
  • epsilon (空文字) 遷移
    • 上記例でいえば、1 から 2 への epsilon 遷移を加えたようなケース
      • ‘b’ から始まる文字列も受理されることになる

一見 DFA よりも NFA の方が強力なモデルに見えるが、両者で受理可能な言語の集合は一致しており計算能力に差異は無い。

計算可能なこと

FSM が行うのは、入力文字列が遷移規則で定義された文字列の集合に属するか、という計算である。このような文字列の集合は言語と呼ばれる。上記例で示したFSM は「 ‘ab’ で始まる文字列を全て含む言語」を認識するといえる。

あらゆる FSM を考えると、FSM で受理可能な言語全体の集合というものを定義できる。FSM で受理可能な言語の集合は正規表現で記述できる言語の集合と一致することが知られており、正規言語と呼ばれる。

計算不可能なこと

FSM は入力文字列が正規言語であるかしか答えられない。例えば四則演算を行うことが不可能。

また正規言語に属さない形式言語に関しても受理可能かを判断することができない。例えば ‘[[]]’ のように開き、閉じ括弧が一致した文字列として定義される言語を FSM で表現することは不可能。