コンピュータ考古学として Version 7 Unix の diff 実装を読んだので理解したことを整理します。 資料や実際のソースコードはページ下部の「参考」項や途中で適宜リンクしています。

diff と LCS

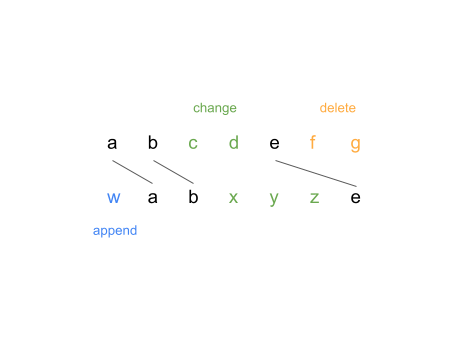
diff アルゴリズムの中核は、行を単位として 2 つのファイル間の LCS (最長共通部分列) を求めることです。例えば abcdefg と wabxyze という内容のファイル (便宜上文字列で表すが実際は各文字で一行とする) を考えた場合、LCS は abe です。それがわかれば前者の文字列から後者の文字列にするための diff 操作は以下のように導くことができます。

  • LCS の要素間を前から順番に見たとき、
    • 後者の文字列にしか要素が含まれないならそれらを append
    • 前者の文字列にしか要素が含まれないならそれらを delete
    • 両者の文字列に要素が含まれるならそれらを change
lcs-to-command

実際の出力:

$ diff one.txt two.txt
0a1
> w
3,4c4,6
< c
< d
---
> x
> y
> z
6,7d7
< f
< g

一つ注意が必要なのは diff では行単位での差異を見たいという点です。そのためそのまま LCS の計算を行うと、その比較に毎回行の比較、つまり文字列の比較が必要になり計算コストが増加します。diff アルゴリズムではそれを避けるために予め各行のハッシュ値を計算し、それを元に LCS を計算します。しかしハッシュ値は異なる文字列で衝突する可能性もあるため LCS 計算後に確認を行い、一致しない場合 (ソースではそれを jackpot と呼んでいる) それを単に除いたものを LCS だとみなして処理を進めます。

(当時は 1 word = 16-bit で 2 年間で 1 度だけ jackpot に気付くことがあったとのこと。現代だと実用上無視できるぐらいの可能性にしかならなさそう)

LCS の計算

LCS を求める代表的なアルゴリズムの一つに 動的計画法によるもの があります。このアルゴリズムは当時から知られていたようですが、時間計算量や空間計算量が O(mn) (m, n をそれぞれ比較するファイルの行数とする) かかることから Version 7 Unix では こちらの論文 を元にしたアルゴリズムが採用されています。

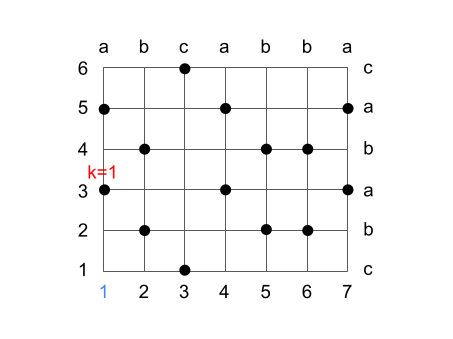
このアルゴリズムについては こちら に詳細な解説もあるのですが、文章だけだとうまくイメージができなかったので、本文中でも使われている文字列 1: abcabba と文字列 2: cbabac の LCS を求める場合を例として処理の流れを整理してみました。

まず前準備として各文字列で共通に使用される文字のインデックスを O(1) で求められるように計算します。例えば文字列 1 の 1 番目の文字 a に対しては文字列 2 の 3, 5 番目というのが求めたいものです。今後はこのような位置を (1, 3), (1, 5) のように各文字列のインデックスで表現します。一致する箇所を求める手順はここでは省略しますが、その関係は以降の図では格子状の黒丸で表されています。

アルゴリズムの大まかな流れは、部分文字列の長さが k となるものを管理しつつ、文字列 1 の前から順番に、それらが最適となるように更新していくというものです。最適、というのは長さ k の部分文字列として採用される文字列 2 の末尾のインデックスが最小となるように選択する、ということです。

まず文字列 1 の 1 番目の文字についてですが、ここでは k=1 の部分文字列として (1, 3) を取るのが最適です。

lcs-algorithm-step1
Step 1

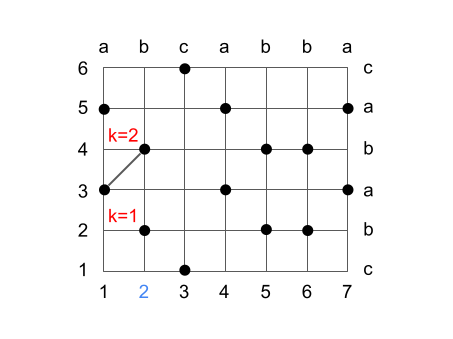
文字列 1 の 2 番目の文字について見ると、一致する位置は (2, 2), (2, 4) となります。k=1 については (2, 2) を採用すると、文字列 2 におけるインデックスの位置を 3 -> 2 に減少できるため (2, 2) で更新します。また前回の k=1 の (1, 3) と合わせて (2, 4) で k=2 を作れるのでこれを k=2 の部分文字列候補とします。

(余談ですがアルゴリズムの実装時にはここで更新した k=1 をそのまま k=2 にも使わないように注意が必要になります。実際の実装では k=1 を更新する前に前の k=1 の情報を oldc, oldl といった変数で管理し、k=2 ではそれを使用しているようです)

lcs-algorithm-step2
Step 2

次のステップでは k=1 を (3, 1) で更新します。k=2 については (3, 6) ではいまより最適なものに更新できない (4->6 になる) ので維持します。新たに k=3 が k=2 の部分列を伸ばして (3, 6) につなげることで作成できるので更新します。

lcs-algorithm-step3
Step 3

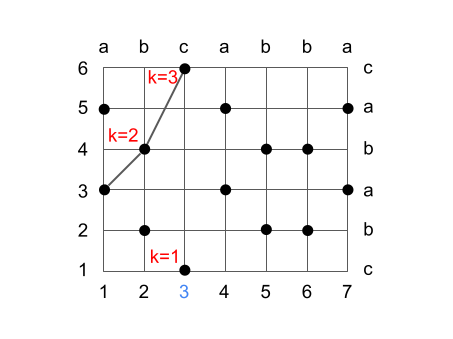
以降のステップも同様に更新していきます。

lcs-algorithm-step4
Step 4
lcs-algorithm-step5
Step 5
lcs-algorithm-step6
Step 6
lcs-algorithm-step7
Step 7

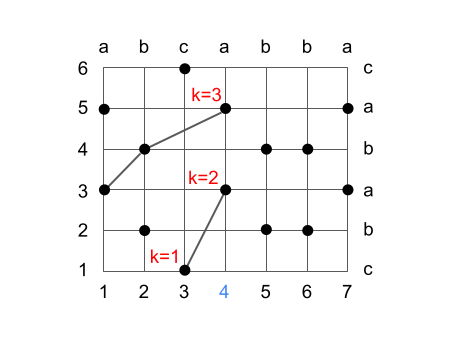
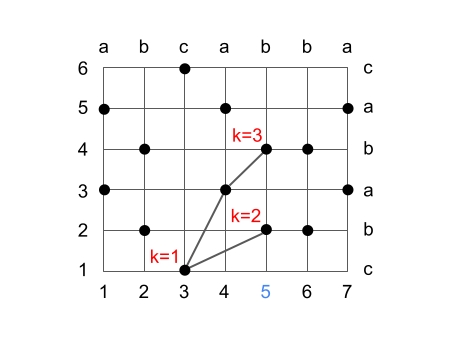
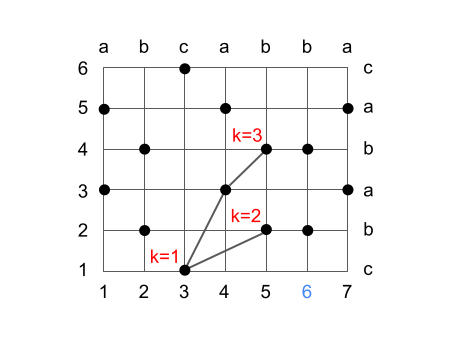
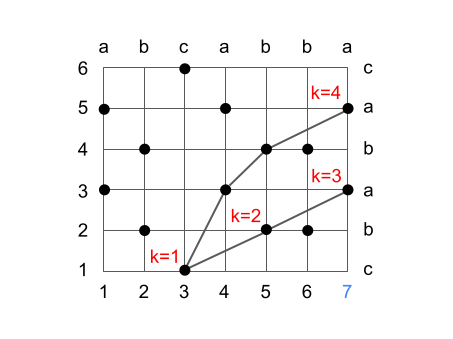
最終的には k=4 の (3, 1), (4, 3), (5, 4), (7, 5) の共通部分列を求めることができ、これは確かに LCS の一つとなります。

このアルゴリズムの計算量ですが、最悪の場合だと時間計算量 O(mnlog(m)) 空間計算量 O(mn) ということで動的計画法のものと変わらないかむしろ悪化しています。比較の必要な候補が増える (上の図でいう黒丸が増える) ほど最悪の計算量に近付くのですが、本文によれば現実的には n よりも候補が多くなることはあまりないとしています。またそのための工夫というのも恐らく diff 実装には入れられていて、例えば LCS の計算前に 2 つのファイルの先頭、末尾で一致する行は予め除くという処理が行われています。これが無い場合同じ文字列をただ毎行繰り返すだけのファイルで diff を取ると最悪の計算量を達成できてしまうと思います。

実際の実装について

実装で一番理解の難しい箇所は上の LCS 計算部分だと思うのですが、折角実装全体を眺めたので備忘録としてその他の部分についても大まかな処理の内容を整理しておきます。diff.c の main から呼ばれる各関数ベースでさらっていきます。

void main(int argc, char **argv)
{
    ...

	filename(&argv[1], &argv[2]);
	filename(&argv[2], &argv[1]);
	prepare(0, argv[1]);
	prepare(1, argv[2]);
	prune();
	sort(sfile[0],slen[0]);
	sort(sfile[1],slen[1]);

	member = (int *)file[1];
	equiv(sfile[0], slen[0], sfile[1], slen[1], member);
	member = (int *)ralloc((char *)member,(slen[1]+2)*sizeof(int));

	class = (int *)file[0];
	unsort(sfile[0], slen[0], class);
	class = (int *)ralloc((char *)class,(slen[0]+2)*sizeof(int));

	klist = (int *)talloc((slen[0]+2)*sizeof(int));
	clist = (struct cand *)talloc(sizeof(cand));
	k = stone(class, slen[0], member, klist);
	free((char *)member);
	free((char *)class);

	J = (int *)talloc((len[0]+2)*sizeof(int));
	unravel(klist[k]);
	free((char *)clist);
	free((char *)klist);

	ixold = (long *)talloc((len[0]+2)*sizeof(long));
	ixnew = (long *)talloc((len[1]+2)*sizeof(long));
	check(argv);
	output(argv);
	status = anychange;
	done();
}

filename, prepare, prune

  • コマンドラインから受け取ったファイル名 2 つから内容を読む (file0, file1)
  • 各行は readhash でハッシュ化した値のみを保存
  • prune では上述したファイル先頭、末尾で一致する行の除外 (pref, suff) も行っている

これらの処理によって struct line *sfile[2] が用意される。line 構造体では serial (行番号) と value (ハッシュ値) を管理する。 sfile[0], sfile[1] がそれぞれ file0, file1 に相当する。

sort

  • sfile[0], sfile[1] を value (ハッシュ値) でソートする

equiv

  • sfile[0] の value を sfile[1] のインデックスに変換する
    • sfile[0], sfile[1] はどちらも value でソートされているので、前から見て一致する sfile[1] のインデックスの値をセットする。一致するのがなければ 0
  • int *member を member[i] が sfile[1][i].serial となるように用意。ただし value が一致する一連の serial において先頭の serial については負とする
    • 例えば sfile[1] が [{serial: 1, value: 1}, {serial: 3, value: 1}, {serial: 2, value: 2}] ならば member = [-1, 3, -2]
    • diff.pdf の解説でいう E にあたるものだと思われる

unsort

  • int *class を file0 の行番号 i から一致する value を持つ sfile[1] のインデックスが class[i] で求められるように用意する
    • diff.dpf の解説でいう P にあたるものだと思われる

stone

  • LCS の計算
    • これまでに用意した member, class を利用する
    • struct cand *clist に部分列の情報が含まれる
      • cand 構造体には file0, file1 の行番号と前の cand を指す clist のインデックスが含まれる
    • klist[i] で長さ i の共通部分列の候補の末尾の cand を指す clist のインデックスを管理

最終的には LCS の長さが k であるとき cand[klist[k]] から前の cand を辿り LCS を再現できる。

unravel, check, output

  • 求めた LCS から diff 出力のための準備
  • check では上述のようにハッシュ値が衝突してしまった場合のケアをしている
  • 実際の出力は output で

参考