AtCoder Begginer Contest 172 D - Sum of Divisors の想定解は \(O(N) \) のようですが、\( O(\sqrt N) \) 解法というのも存在し、こちら の (4) でより詳細な解説を見ることができます。ただ自分のように格子点に馴染みの無い人間にはこれだけだと理解が難しかったので、補足として自分なりに考えて納得した道筋を書いておきます。

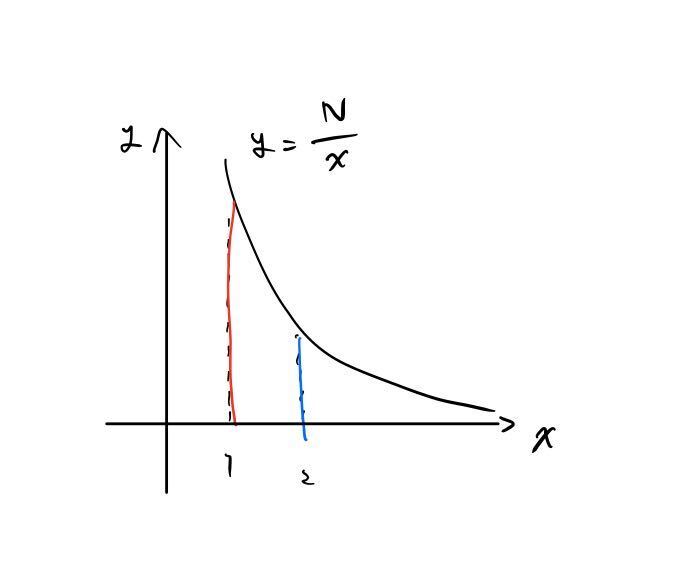
まずは \( y = \frac{N}{x} \) のグラフを使用して \( O(N \log{N}) \) あるいは \( O(N) \) 解法がどういったものだったかをおさらいします。x を約数と見て固定したとき、\( y \le \frac{N}{x} \) を満たす正整数 \( y \) は \( x \) を約数に持つ数です。例えば x = 1 のときは y = 1, 2, 3, … N が条件を満たす数で、x = 2 のときは y = 2, 4, 6, … N (あるいは N - 1) となります。問題の答えは各 x についてこのような条件を満たす y を求めてその和を足し合わせたものです。言い換えると「x >= 0 かつ y >= 0 かつ xy <= N を満たす全ての正整数の組 (x, y) を求め、その y の和を求める」ということです。グラフでいうとまずは x = 1 (図中赤線) 上の格子点を求め、次に x = 2 (図中青線) 上の格子点を求め、… のようになります。計算量としては各 x について \(O(\log{N}) \) あるいは \( O(1) \) で計算できるので全体で \( O(N \log{N}) \) あるいは \( O(N) \) となります。ちなみに格子点の数自体は \( O(N \log{N}) \) です。

graph for solution of O(N)

C++ のコード例は以下のようになります。

// O(N * logN)
int main(void) {
    int N;
    cin >> N;

    ll ans = 0;
    ll cnt = 0; // 条件を満たす格子点数のカウント
    for (int i = 1; i <= N; i++) {
        for (int j = i; j <= N; j += i) {
            ans += j;
            cnt++;
        }
    }

    // printf("ans: %lld, cnt: %lld\n", ans, cnt);
    cout << ans << endl;

    return 0;
}

\( O(\sqrt{N}) \) 解法では数え上げる順序を 「min(x, y) が 1 から \( \sqrt{N} \)」 となるようにします。図のようにまずは min(x, y) = 1 (赤の実線) 上の格子点について計算し、次に min(x, y) = 2 (青の実線) 上の格子点について計算します。

graph for solution of O(sqrt(N))

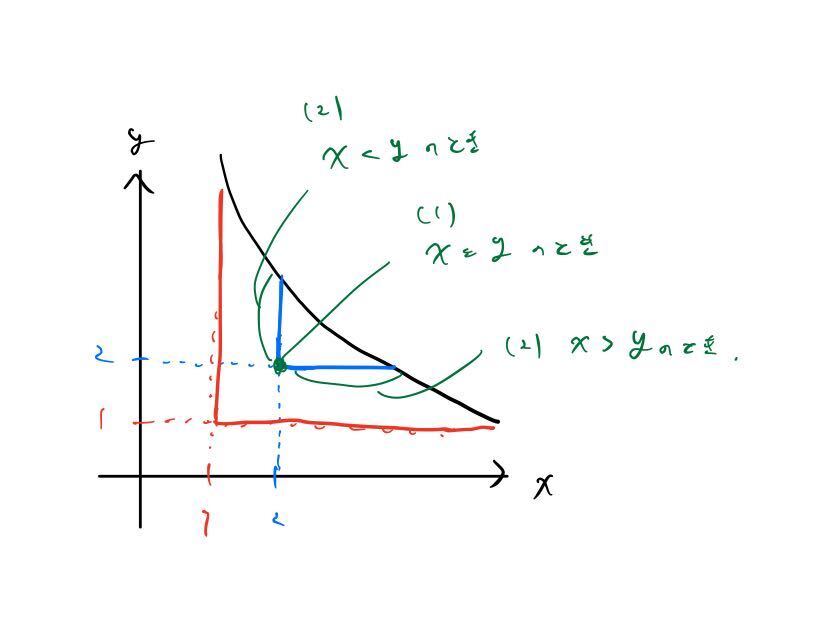
C++ のコード例は以下の通りです。図中の緑で示した (1), (2) とコード例の (1), (2) を対応させています。格子点の数え上げ方を変えることで計算量を落とせるというのは何だか不思議ですが図にするとなるほど、と思いました。

// O(sqrt(N))
// ref. https://maspypy.com/atcoder-%E5%8F%82%E5%8A%A0%E6%84%9F%E6%83%B3-2020-06-27abc-172#toc4
int main(void) {
    int N;
    cin >> N;

    // 1 + 2 + 3 + ... + n
    auto f = [](const ll n) {
        return n * (n + 1) / 2;
    };

    ll ans = 0;
    for (int i = 1; i * i <= N; i++) {
        // (1) x == y
        ans += i * i;

        // (2) x < y or x > y
        ans += 2 * i * (f(N / i) - f(i));
    }

    cout << ans << endl;

    return 0;
}