Linux の IP チェックサム計算処理を読む
IP のようなネットワークプロトコルではデータの破損を検出するためにチェックサムが使用されます。 このアルゴリズムの概要を確認し、Linux における実装を見ていきます。
チェックサムアルゴリズム概要
チェックサム計算アルゴリズムに関する RFC は RFC 1071 です。 アルゴリズムの概要は以下のようになっています。
パケット送信者:
- チェックサム格納領域 (例えば
struct ipにおけるip_sum) を 0 埋めする - チェックサム計算対象領域 (例えば IP の場合 IP ヘッダ) で 16 bit 毎に 1 の補数表現による加算を行う
- 計算結果の 1 の補数をチェックサム格納領域に入れる
パケット受信者:
- チェックサム計算対象領域で 16 bit 毎に 1 の補数表現による加算を行う
- 計算結果が -0 (全 bit が 1) となることを確認する
1 の補数和 (1 の補数表現における加算) というのが馴染み薄いので少し整理します。そもそも補数とはなにかという話ですが、「ある自然数のセットに正負の整数を対応させるやり方の一つ」という見方ができると思います。n 桁の b 進数で表現される数において、例えば 1 <= y < (b^n)/2 となる y の補数は b^n - y で表され、これを -y とする、そうすると減算も加算と同じアルゴリズムで計算できる、ということでコンピュータサイエンスでよく登場する概念です。特によく聞くのは b=2 の場合でこれを 2 の補数表現と呼びます。
1 の補数表現というのは 2^n - y ではなく (2^n - 1) - y を補数とみなす表現です。 (2^n - 1) - y は n 桁の bit を反転させた数なので補数を求めやすく、また (2^n - 1) - y + 1 は 2^n - y なので 1 の補数を求めてから 1 を足して 2 の補数を求める、というのはよく聞くアルゴリズムです。
このあたりについては IP チェックサムの秘密 の前半が参考になります。
IP チェックサム計算においては 2 の補数ではなく 1 の補数が使用されますが、1 つの理由としては endianness を気にせず計算できるというのがあるようです。これは感覚的には以下のように理解しています。
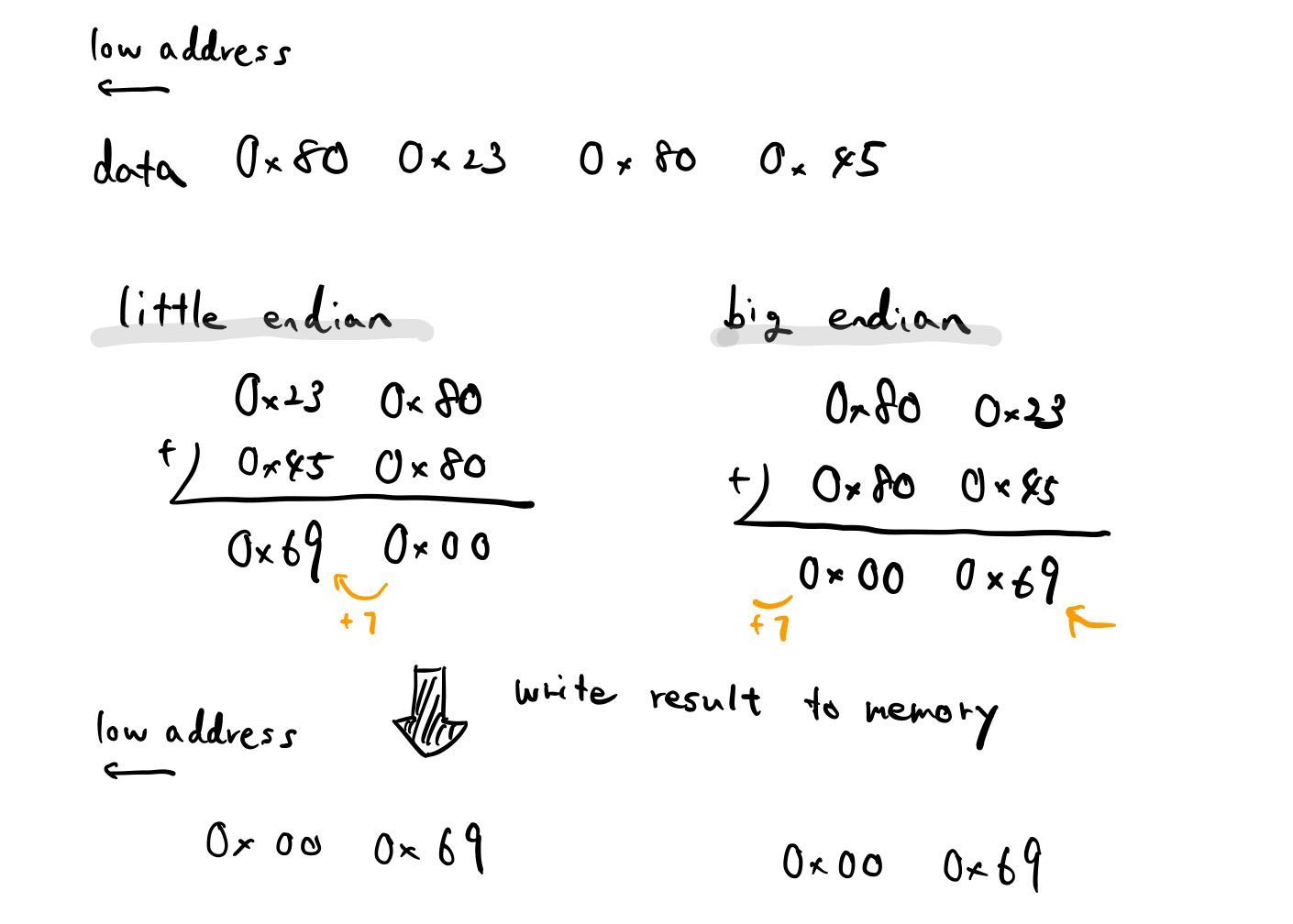
Linux ソース該当箇所
Linux ソースコードをざっと見た感じチェックサム計算を行う関数は lib/checksum.c の do_csum のようです。過去のコミット等を読むとこのファイルでは cpu アーキテクチャによらない generic な実装を提供しているようです。アーキテクチャ毎に最適化した実装を提供する場合もあり、それは多分 arch/<arch>/lib/checksum.c で定義されています。
ここでは説明のために do_csum だけを引用します。
static inline unsigned short from32to16(unsigned int x)
{
/* add up 16-bit and 16-bit for 16+c bit */
x = (x & 0xffff) + (x >> 16);
/* add up carry.. */
x = (x & 0xffff) + (x >> 16);
return x;
}
static unsigned int do_csum(const unsigned char *buff, int len)
{
int odd;
unsigned int result = 0;
if (len <= 0)
goto out;
odd = 1 & (unsigned long) buff;
if (odd) {
#ifdef __LITTLE_ENDIAN
result += (*buff << 8);
#else
result = *buff;
#endif
len--;
buff++;
}
if (len >= 2) {
if (2 & (unsigned long) buff) {
result += *(unsigned short *) buff;
len -= 2;
buff += 2;
}
if (len >= 4) {
const unsigned char *end = buff + ((unsigned)len & ~3);
unsigned int carry = 0;
do {
unsigned int w = *(unsigned int *) buff;
buff += 4;
result += carry;
result += w;
carry = (w > result);
} while (buff < end);
result += carry;
result = (result & 0xffff) + (result >> 16);
}
if (len & 2) {
result += *(unsigned short *) buff;
buff += 2;
}
}
if (len & 1)
#ifdef __LITTLE_ENDIAN
result += *buff;
#else
result += (*buff << 8);
#endif
result = from32to16(result);
if (odd)
result = ((result >> 8) & 0xff) | ((result & 0xff) << 8);
out:
return result;
}
do_csum を見ると確かに alignment のために endianness による分岐の入る箇所 (__LITTLE_ENDIAN ディレクティブによる分岐が入る箇所) がありますが、チェックサム計算自体は endianness に依存しない処理になっていることがわかります。
チェックサム計算のメイン部は do while で囲まれた部分です。16 bits 毎ではなく 32 bits 毎に加算を行い、最後にそれを 16 bits の計算値にするというやり方は RFC の Numerical Examples に紹介されているやり方と同様です。これは 1 の補数による加算が結合性を持ち可換であるために行えるやり方です (可換の必要性は RFC で明確に言及されていないのでやや自信ない)。
RFC の内容をざっと理解していればそこまで難しい内容ではないですが、細かいところで do_csum の実装でわかりづらい箇所が 2 つあったので最後にそれに触れます。
carry = (w > result)- これは直前で
result += wしていることを踏まえると、不等号が成立するのは result が桁溢れした場合のみのはず。桁溢れしたので次回の計算で carry を加えようねということ
- これは直前で
- 最後の方の
if (odd)- これは具体例を考えれば感覚的には納得できる。
do_csum開始直後のif (odd)の分岐に入った場合、本来下位 1 byte の結果になるべきものが上 1 byte 側に入ってしまうので、swap して調整しているという理解
- これは具体例を考えれば感覚的には納得できる。
