JSON number や浮動小数点数の話
JSON といえば Web API であったり様々な箇所でお馴染みのデータフォーマットです。最近 play-json という Scala の JSON ライブラリについて話をしたときに、 昔 JSON の number 処理でハマったことがあったのを思い出したので、改めて調べた内容をメモしておこうと思いました。
1. ハマった内容
文章で説明すると「JSON で絶対値の大きい整数を number として記述した場合に、同じ JSON なのにそれを処理するプログラム (あるいは言語やライブラリ) によって結果が異なる」というものです。
具体例としては JSON number で表記した 9007199254740999 をパーズした場合、
JavaScript (Google Chrome v72.0) だと
> JSON.parse("9007199254740999");
9007199254741000
のように丸められた値が返されますが、
play-json (v2.7.2 ただしデフォルト設定) の場合、
scala> Json.parse("9007199254740999")
res3: JsValue = 9007199254740999
のように正確に扱えるというように実装によって違いが出ています。
2. JavaScript の挙動の理由
- JSON の number が ECMAScript の Numbers に対応
- ECMAScript の Numbers が IEEE 754 の倍精度浮動小数点数として扱われる
というのが理由になります。
1 つ目については ECMAScript の仕様 Json.parse 項を見ると
JSON strings, numbers, booleans, and null are realized as ECMAScript Strings, Numbers, Booleans, and null.
ということで JSON の number は ECMAScript でいう Numbers に対応することがわかります。
2 つ目については ECMAScript 仕様の Number value 項に明記されています。
IEEE 754 の定める浮動小数点数については既に広大なネットの海に学ぶための材料は存在すると思うので省略します。ここで重要な点は
- 倍精度浮動小数点数は符号部 1 bit, 指数部 11 bits, 仮数部 52 bits で構成される
- 表現できる数ならばその表し方は 1 通りのみ
- 絶対値が大きくなるほど表現できる数同士の差が大きくなる
だと思います。3 点目については少しわかりにくいかもしれませんがこの理解を x + 0.25 - 0.25 = xが成り立たないxとは何か で知り浮動小数点数についてのイメージがだいぶ掴めた覚えがあります。
例えば倍精度浮動小数点数では 1 という数字は以下のように表現されます。
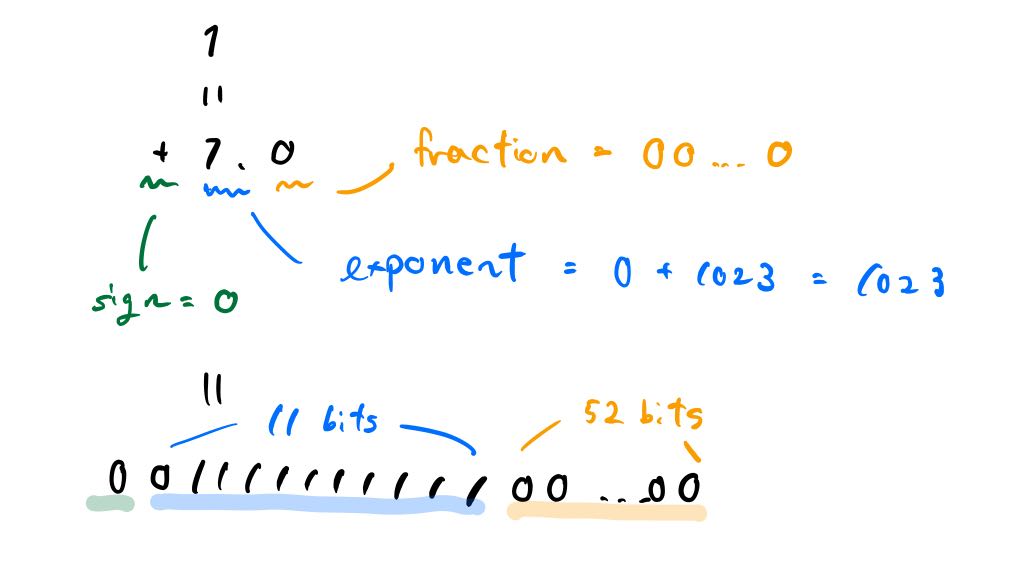
このとき 1 の次に大きく、かつ倍精度浮動小数点数で表現できる数は
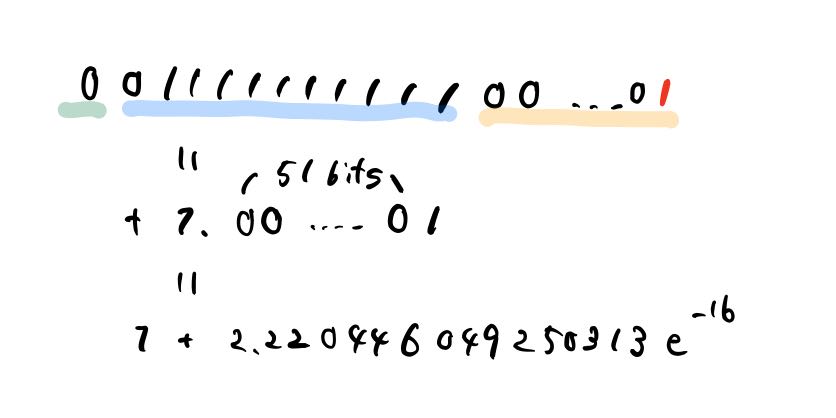
のように 1 + 2.220446049250313e^-16 という数になります。この数からしばらくは同様の差で次の点が出現する (仮数部を 1 ずつ増やした数) のですが、仮数部 52 bits が全て 1 になると次の数は指数部が 1 増え仮数部は 0 になり (数としては 2)、以降の数同士の差は 2 倍になります。

これを繰り返して 2^52 という数に達するとそれ以降表現できる数同士の差は 1 となります。

そして仮数部の全 bit が 1 である 2^53 - 1 という数を超えると、指数部が 1 増え表現できる数同士の差は 2 になります。つまりこの時点で正確な整数を表現できなくなるということですね。
いまは正の整数のみを考えましたが、浮動小数点数では符号部の 0, 1 で正負を表現するだけなので、全く同じ話が負の数にも言えるはずです。なので倍精度浮動小数点数で正確に表現できる数の範囲というのは -(2^53 - 1) から 2^53 - 1 ということになります。
ECMAScript ではこの上限下限を Number.MAX_SAFE_INTEGER と Number.MIN_SAFE_INTEGER として明示しています。
> Number.MAX_SAFE_INTEGER
9007199254740991
> Number.MIN_SAFE_INTEGER
-9007199254740991
あまりわかりやすい説明にならなかったかもしれませんが、以上の内容については他に javascript ではなぜ 2^53 - 1 以下の整数を正確に表せるのか の内容も参考になるかもしれません。
またここで例に出した浮動小数点数の表記等は手で書いて確認しているのですが、それだけだと少し不安だったので Julia の REPL でも確認しています。整数と浮動小数点数 で触れられているように Julia ではある浮動小数点数と次の表現できる数との差 (epsilon) やその bit 表現を簡単に出力することができるので助かりました。
3. play-json の挙動の理由
- play-json の JsValue データ型では number を BigDecimal で表現する
というのが理由になります。
play-json では JsValue というデータ型で JSON を表現します。 これは簡略すると以下のように定義されます。
case object JsNull extends JsValue
case class JsBoolean(value: Boolean) extends JsValue // 簡略。ライブラリでは JsTrue, JsFalse というオブジェクトが sealed absract class JsBoolean を継承するという形
case class JsNumber(value: BigDecimal) extends JsValue
case class JsString(value: String) extends JsValue
case class JsObject(value: Map[String, JsValue]) extends JsValue
case class JsArray(value: IndexedSeq[JsValue]) extends JsValue
このうち JSON の number に対応するのが BigDecimal を持つ JsNumber です。 BigDecimal は任意精度の小数を表現するためのデータ型です。play-json ではこの精度を設定として渡したりできそう (実装を見る感じ) なのですが、デフォルトでもそれなりの精度を持つらしく倍精度浮動小数点数では正確に表現できない整数も表現できる、というのが上で見た挙動の違いになります。
4. JSON の number 仕様
ということで JSON の number というのは処理するプログラムによって解釈が異なり得るのですが、JSON というデータフォーマットとしてはどういう仕様になっているのか確認しました。
JSON については RFC 8259 で仕様が定義されており、number については 「6.Numbers」 項に以下のような記述があります。
This specification allows implementations to set limits on the range and precision of numbers accepted
ということで JSON というフォーマット自体には特に数値の上限下限、精度についてはそれを処理するプログラムが任意に決めてよいようです。ただ同時に
Since software that implements IEEE 754 binary64 (double precision) numbers [IEEE754] is generally available and widely used, good interoperability can be achieved by implementations that expect no more precision or range than these provide, in the sense that implementations will approximate JSON numbers within the expected precision
とも言及されています。これは JavaScript のように倍精度浮動小数点数として解釈するのが無難じゃないか、という感じみたいですね。
ということで JSON の number の精度は特に仕様がなく解釈するプログラムによって変わりうるという話でした。上の例のように絶対値の大きい整数を扱う場合は Twitter IDs (snowflake) がそうしているように文字列として渡すべきということになるかと思います。