チューリングマシンについて

チューリングマシンについての個人的なまとめです。

チューリングマシン (Turing Machine, TM)

チューリングマシンは計算論において最も重要な計算モデルの一つである。この仮想的な機械は無限長のマス目を持つテープとその上を動くテープヘッド、現在の状態から構成される。遷移規則をもとに与えられた入力が受理可能かを判断するという点では有限状態機械と同様だが、それが計算可能とする問題の範囲は広い。

チューリングマシンの遷移規則は以下の要素から成る。

機械の現在の状態
テープヘッドの現在の位置の文字
機械の次の状態
テープヘッドの現在の位置に書き込む文字
書き込み後、ヘッドを動かす方向 (右 or 左)

チャーチ・チューリングのテーゼでは、計算可能な関数をチューリングマシンで計算可能とする関数のクラスと同一視しており、チューリングマシン以上の能力を持つ計算モデルは存在しないと推測している。

チューリングマシンの例

2進数で表された自然数を increment するチューリングマシンは以下のように表現される。矢印は遷移規則を表し、そのラベルは <テープヘッド先の文字>/<テープヘッド先に書き込む文字>, <テープヘッドを動かす方向> という表記になっている。

turing machine

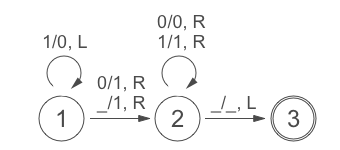
上記チューリングマシンの動作をプログラムで実装すると以下のようになる。

from collections import namedtuple
from enum import Enum

class Direction(Enum):
    LEFT = 1
    RIGHT = 2

class TMRule(namedtuple('TMRule', ['start_state', 'read_char', 'next_state', 'write_char', 'move_dir'])):
    '''
    Transition rule of turing machine.
    '''
    __slots__ = ()

    def is_applied_to(self, config):
        '''
        Return True if this rule can be applied to the current TMConfiguration.
        '''
        return config.state == self.start_state \
                and config.tape.current_char() == self.read_char

    def apply(self, config):
        '''
        Apply this rule to the current TMConfiguration and return a new TMConfiguration.
        '''
        new_state = self.next_state
        if self.move_dir == Direction.LEFT:
            new_tape = config.tape.write_char(self.write_char).move_left()
        else:
            new_tape = config.tape.write_char(self.write_char).move_right()
        return TMConfiguration(new_tape, new_state)

class Tape(namedtuple('Tape', ['cells', 'current_pos', 'blank_char'])):
    '''
    Tape with infinite cells.
    '''
    __slots__ = ()

    def current_char(self):
        '''
        Return a character at the current position.
        '''
        return self.cells[self.current_pos]

    def write_char(self, char):
        '''
        Write a character at the current position.
        '''
        new_cells = list(self.cells)
        new_cells[self.current_pos] = char
        return Tape(new_cells, self.current_pos, self.blank_char)

    def move_left(self):
        '''
        Move the tape head to left.
        Empty cell is added to the left side if necessary.
        '''
        new_cells = list(self.cells)
        if self.current_pos == 0:
            new_cells = [self.blank_char] + new_cells
            return Tape(new_cells, self.current_pos, self.blank_char)
        else:
            return Tape(new_cells, self.current_pos - 1, self.blank_char)

    def move_right(self):
        '''
        Move the tape head to right.
        Empty cell is added to the rithg side if necessary.
        '''
        new_cells = list(self.cells)
        if self.current_pos >= len(self.cells) - 1:
            new_cells = new_cells + [self.blank_char]
            return Tape(new_cells, self.current_pos + 1, self.blank_char)
        else:
            return Tape(new_cells, self.current_pos + 1, self.blank_char)

class TMConfiguration(namedtuple('TMConfiguration', ['tape', 'state'])):
    __slots__ = ()

class DTM:
    '''
    Simulator of deterministic turing machine.
    '''
    def __init__(self, initial_state, rules, accept_states):
        self.initial_state = initial_state
        self.rules = rules
        self.accept_states = accept_states

    def does_accept(self, string):
        '''
        Return True if a passed string is in the language of this turing machine.
        '''
        tape = Tape(string, len(string) - 1, '_')
        config = TMConfiguration(tape, self.initial_state)
        while True:
            if config.state in self.accept_states:
                return (True, config)
            appliable_rule = self.lookup_appliable_rule(config)
            if appliable_rule is None:
                return (False, config)
            config = appliable_rule.apply(config)

    def lookup_appliable_rule(self, config):
        available_rules = [ x for x in self.rules if x.is_applied_to(config) ]
        if len(available_rules) == 0:
            return None;
        return available_rules[0]

if __name__ == '__main__':
    # transition rules to increment binary digits
    rules = [ TMRule(1, '1', 1, '0', Direction.LEFT), \
              TMRule(1, '0', 2, '1', Direction.RIGHT), \
              TMRule(1, '_', 2, '1', Direction.RIGHT), \
              TMRule(2, '1', 2, '1', Direction.RIGHT), \
              TMRule(2, '0', 2, '0', Direction.RIGHT), \
              TMRule(2, '_', 3, '_', Direction.LEFT), \
              ]

    # create turing machine
    dtm = DTM(1, rules, [3])

    # (True, TMConfiguration(tape=Tape(cells=['0', '1', '0', '_'], current_pos=2, blank_char='_'), state=3))
    print(dtm.does_accept('001'))
    # (True, TMConfiguration(tape=Tape(cells=['1', '1', '0', '0', '_'], current_pos=3, blank_char='_'), state=3))
    print(dtm.does_accept('1011'))
    # (True, TMConfiguration(tape=Tape(cells=['1', '0', '0', '0', '_'], current_pos=3, blank_char='_'), state=3))
    print(dtm.does_accept('111'))
    # (False, TMConfiguration(tape=Tape(cells=['1', '2', '0'], current_pos=1, blank_char='_'), state=1))
    print(dtm.does_accept('121'))

万能チューリングマシン (Universal Turing Machine, UTM)

「遷移規則と処理対象の文字列を一つの入力として受け取り、規則で記述された計算を実行する」ことができるチューリングマシンを考える。この機械は入力の規則を変えるだけであらゆるチューリングマシンで行える計算が実行可能であり、いわばチューリングマシンのインタプリタのような機能を持つ。

このような機械は実際に作成可能であり、万能チューリングマシンと呼ばれる。

計算可能なこと

上述のように一般的に計算可能とする関数とチューリングマシンで計算可能な関数のクラスは一致する。そのため有限状態機械やプッシュダウンオートマトンで計算可能な関数は全てチューリングマシンでも計算可能である。計算可能な関数が持つ性質については計算可能関数についてにまとめている。

他に計算可能な関数の具体例としては原始再帰関数が挙げられる。簡単な原始再帰関数としては以下のようなものがある。

自然数の可減乗除
i 番目の素数を求める関数

計算不可能なこと

代表的なものとして停止性問題が挙げられる。