「コンパイラ」読書メモ

少し前からHaskellのparsecというパッケージを触っていたのですが、それに触発されてコンパイラという本を読み始めました。

本の記載のうち留めておきたい内容や自身のまとめたこと、考えたことなどをまとめてみます。なお、本書の記述による部分と自身の追記が混在しているため、追記であることを明示したい部分には ‘t>’ を付記しています。

まえがき

本書はPL/0と言うプログラミング言語(に少し機能を足したもの)用のコンパイラを作成しながら、コンパイラの理論を学ぶためのテキストである
本書で作成するコンパイラの目的コードは、機械語ではなくスタックを持った仮想マシン上で実行することを想定した後置記法型のコードである
- t> そのため直接機械語を生成したいといった場合は、別のテキストも読むことを進めている
コンパイラ、仮想マシンともにC言語で実装しており、実装全体が本書末尾に付録されている

1. コンパイラの概要

コンパイラ(compiler)

高級プログラミング言語を機械向き言語に変換するためのプログラム
- t> 機械向き言語、とはあまり聞き慣れない単語だけれど、機械語、アセンブリ言語、また高級プログラミング言語が用意しているVM上で動作させるための言語といったものを含めるためにこう呼んでいるっぽい
コンパイラ元のプログラムを原始プログラム(source program)、変換後のコードを目的プログラム(target program)と呼ぶ
t> e.g. 処理系(言語): GFortran(FORTRAN), gcc(C), SBCL(Common LISP), GHC(Haskell)

インタプリタ(interpreter)

原始プログラムを一度中間語に変換し、これを原始言語のために用意したVM上で解釈実行を行うプログラム
中間語に変換するタイミングとしては実際にプログラムを実行するより前か実行中にというパターンがある
t> ちなみにWikipediaでは以下のように区分されている
- 1.は今ではあまり見ないが、2.はPython, Ruby等、3.はJavaや.NET Frameworkが例に挙げられている

ソースコードを直接実行する。

ソースコードを何らかの効率的な中間表現に変換しながら実行する。

システムの一部であるコンパイラが生成し出力した、コンパイル済みの中間表現を実行する。ソースプログラムはマシンに依存しない中間的なコードに事前にコンパイルされ、実行時にリンクされ、インタプリタで実行される。

実行時コンパイラ(Just-In-Time compiler, JIT compiler)

t> 本には記載のない内容だが、実行時にコンパイルという方法もある
- 表面上はインタプリタのような動作に見えるが、実際は機械語を生成、実行している
- インタプリタと直交する概念ではなく、インタプリタの中にはこんなことをする奴もいるよとという感じ
- e.g. 各種ウェブブラウザのJavaScript処理系。 JVM(HotSpot、使用回数の多いメソッドのみコンパイルする)

疑問

Javaとか.NETの処理系って一般的にはインタプリタとは呼ばれてない気がする
- というか処理系毎に色々やり方がありコンパイラ、インタプリタという区分が結構難しい気が
- ざっくり整理すれば、(現状)以下の3パターンに分けられると思えばいいのでは
  - 実行前に原始プログラムを機械語に変換し、実行時はそれを起動する
  - 実行前に原始プログラムを中間語に変換し、実行時は中間語を入力とする専用の仮想マシン上で実行する
  - 実行時に原始プログラムを入力とし、専用の仮想マシン上で実行する
ある言語の処理系がその言語で書かれているという関係はどのように解決されているのか (e.g. Cで書かれたCのコンパイラ)?
- ‘bootstrap’と呼ばれる手法で解決している
- 仮にある言語 ‘Foo’ のコンパイラを作る場合を考える
  - まずはすでにある別の言語(e.g. C, assembly, machine codes)で必要最小限の機能を持つFoo用コンパイラを書く
  - ‘Foo’言語でFoo用コンパイラを書き、上のコンパイラでコンパイルする -> 完成
  - 次version開発時も前versionのコンパイラ in Fooを使用してコンパイルすればよい
- Bootstrapping a language
- Writing a compiler in its own language

2. コンパイラの簡単な例

後置記法

いわゆる逆ポーランド記法。
中置記法で2*3+5*4と表される場合、後置記法では23*54*+となる
後置記法による表記は計算機にとって扱いやすい

スタック

「Last-In-First-Out(LIFO)」
例えば入れ子になった括弧構造の解析に適している
例えば木構造の解析に適している
後置記法で表された処理に適している

スタックを使用した処理例

スタックを用いて逆ポーランド記法で表記された式の計算を行うPythonプログラムは以下のように書ける。

operators = {
    '+': 6,
    '-': 6,
    '*': 7,
    '/': 7,
}

def calc_rpn(rpn):
    '''
    Evalute a reverse polish notation.

    > calc_rpn(['2', '3', '2', '*', '5', '3', '*', '+', '*'])
    42.0
    '''
    assert rpn is not None
    assert len(rpn) > 0

    stack = []
    while len(rpn) > 0:
        elem = rpn.pop(0)
        if elem in operators.keys():
            expr2 = stack.pop()
            expr1 = stack.pop()
            if elem == '+':
                stack.append(expr1 + expr2)
            elif elem == '-':
                stack.append(expr1 - expr2)
            elif elem == '*':
                stack.append(expr1 * expr2)
            elif elem == '/':
                stack.append(expr1 / expr2)
            else:
                raise RuntimeError('Invalid operator: ' + elem)
        else:
            stack.append(float(elem))
    return stack[0]

スタックを用いて中置記法の式を後置記法の式に変換するプログラムをPythonで書くと以下のようになる。

def convert_to_rpn(elems):
    '''
    Convert a polish notation to reverse polish notation.

    > convert_to_rpn(['2', '*', '(', '3', '*', '2', '+', '5', '*', '3', ')'])
    ['2', '3', '2', '*', '5', '3', '*', '+', '*']
    '''
    assert elems is not None

    if len(elems) == 0:
        return []

    accum = []
    stack = []
    while len(elems) > 0:
        elem = elems.pop(0)
        if elem == '(':
            accum = accum + convert_to_rpn(elems)
        elif elem == ')':
            break
        elif elem in operators.keys():
            while len(stack) > 0 and operators[stack[-1]] >= operators[elem]:
                op = stack.pop()
                accum.append(op)
            stack.append(elem)
        else:
            accum.append(elem)
    while len(stack) > 0:
        op = stack.pop()
        accum.append(op)
    return accum

実際の目的コードを使用した処理例は8章で記載。

2.4 コンパイラの論理的構造

コンパイラの一般的な動作の解説。あくまで一般的(理論的)な構造であり、実際の構造は多岐にわたる(コンパイラの物理的構造の節)。

以下は本文図2.1 コンパイラの論理的構造からの引用である。

compiler-logical-structure

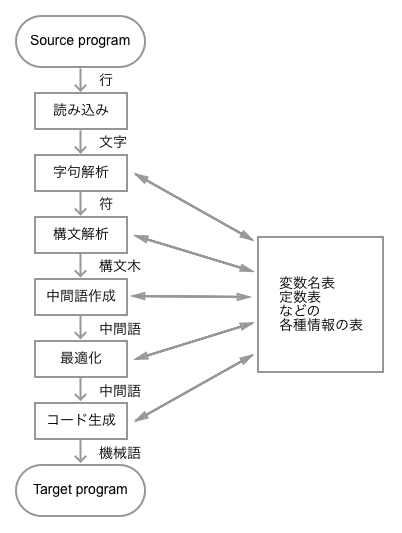
疑問

数式の中置記法から後置記法への変換もシンプルなコンパイラだといえる？
- 解釈に依るのだろうけど、コンパイラと呼べるのでは。1章の説明ではコンパイラを「高級プログラム言語を機械向き言語に変換する変換系」と定義している。中置記法から後置記法への変換は間違いなく変換系ではあるので、中置記法を(簡単な数式計算のみを行うための)プログラム言語とみなし、後置記法に変換されたものを機械向き(ある仮想マシン向きの)言語とみなせるのであれば、それをコンパイラと呼んでも間違いではない気がする。

3. 文法と言語

コンパイラを作成するためには原始言語の構文を厳密に定義する必要がある。本章ではプログラミング言語の構文規則を記述する方法としてBNF(Buckus Naur Form, バッカス記法)と構文図式について説明されている。

バッカス記法、構文図式

詳細は本書やWikipediaを参照。一例として0以上の整数の四則演算から成る式(e.g. (1+2)*5+3)を表す構文規則をBNFで以下に表現する。(厳密には下記のものは拡張BNFとなる)

expr          ::= <term>, { ('+', <term>) | ('-', <term>) }
term          ::= <factor>, { ('\*', <factor>) | ('/', <factor>) }
factor        ::= ('(', <expr>, ')') | <number>
number        ::= <no-zero-digit> { , <digit> }
no-zero-digit ::= '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9'
digit         ::= '0' | no-zero-digit

文法と言語の形式的定義

以降の説明に必要な文法や言語の定義が説明されている。詳細はこれも本書を参照。

ざっくりといえば先述のBNFで定めた各構文規則を生成規則(production)、それらにより定義された構文規則のまとまりを文法(正しくは文脈自由文法, context-free grammerとしている)と定義している。

文脈自由文法 \( G \) は一連の構文規則 \( P \) と開始記号 \( S \in P \) から成るとし、\( G = \{ P, S \} \) と表記する。またここでは生成規則に現れる記号全ての集合を語彙 \( V \) 、その部分集合である非終端記号(nonterminal symbol)の集合を \( V_N \) 、終端記号(terminal symbol)の集合を \( V_T \) と表記することにする。

先述の四則演算から成る式の文脈自由文法は以下のように表現できる(ただし出現する数字は1-9までに限定している)。

G   = { P, E }
P   = { E -> E, '+', T
        E -> E, '-', T
        E -> T
        T -> T, '*', F
        T -> T, '/', F
        T -> F
        F -> '(', E, ')'
        F -> '1'
        ...
        F -> '9'
      }
V_N = { E, T, F }
V_T = { '+', '-', '*', '/', '(', ')', '1'..'9' }
V   = { E, T, F, '+', '-', '*', '/', '(', ')', '1'..'9' }

生成規則 \( E \) から変換(生成)され、終端記号のみからなる記号列を文と定義し、文脈自由文法 \( G \) の文の集合を言語 \( L(G) \) と呼ぶ。例えば上述の文法における \( 1 + 2 * 5 \) は文である。

E => E + T => T + T => T + T * F => F + F * F => 1 + 2 * 5

ちなみに途中の \( E + T \) 等は文形式と定義している。

t> この節の内容は「形式言語理論」と呼ばれる分野になるよう。形式言語とは自然言語と異なり機械的に文構造が処理できる言語のこと。身近な例でいえば全てのプログラミング言語は形式言語。

構文木

ある文法 \( G \) の文が開始記号 \( E \) から生成される様子を図に表すと構文木(parse tree)が得られる。
コンパイラの仕事の一つは与えられた文の構造を調べること、つまり構文木を生成すること(構文解析)。
複数通りの構文木が考えられる場合、その文法をあいまいであるという。
- あいまいな文法は構文解析上嬉しくないので、以下のいずれかで解決する。
  - 新たな生成規則を追加する。
  - 解析を行う上での規則を追加する(e.g. +演算子は左結合性とみて解析する)。

上述の文1 + 2 * 5を構文木で表した一例は以下のようになる。

    E
    |
 +--+---+  
 |  |   |
 E '+'  T
 |      |
 T   +--+--+
 |   |  |  |
 F   T '*' F
 |   |     |
'1'  F    '5'
     |
    '2'

疑問

BNFと文脈自由文法の関係は?
- BNFは文脈自由文法を記述するためのメタ言語
- BNFによって文脈自由文法を表現できるし、逆に文脈自由文法であればBNFで書ける(はず)
- BNFは文法を人間にわかりやすく書くための記法だと思えば良さそう

4. 字句解析

コンパイラが最初に行う仕事は原始プログラムを字句解析し、字句を読み出すことである。字句とは「プログラム上で意味のある最小の構成単位(e.g. 変数名、定数、キーワード、演算記号)」であり、これが構文解析での処理単位となる。本章では字句の定義を正規表現で定義し、その字句を読み取るプログラムを作成するための手順が解説されている。

文字読み取り

原始プログラムからの読み取りを抽象化する関数(nextChar)を定義、解説している。コンパイラはこの関数によって原始プログラムから一文字ずつ読み取りを行う。

正規表現

文字セット \( A \) 上の正規表現とは以下の規則によって作られる表現である。

\( \epsilon \) (空記号列)は正規表現である
\( a \in A \) は正規表現である
\( R, S \) が正規表現ならば、\( R | S, RS, R^* \) も正規表現である

正規表現を文法(3章で定義した)として言語が定義できる(正規文法による言語の定義、詳細は本書参照だが直感通り)。正規文法で定義された言語を正規言語と呼ぶ。

一例として \( L(c(cb|a) ^* b) = \{ c \} \{ cb, a \} ^* \{ b \} = \{ cb, ccbb, cab, .. \} \) となる。

なお本書に関わる内容でいうと、以下の4つは同値である。

対象言語が正規言語である
対象言語が正規表現で表される
対象形式言語が決定性有限オートマトンによって受理可能
対象形式言語が非決定性有限オートマトンによって受理可能

t> 実用的な面でしか扱ったことが無くて知らなかったけれど、正規表現は形式言語理論において正規言語を表すために定義されたものらしい。

非決定性有限オートマトン

有限オートマトン(finite automaton)は、有限個の内部状態を持ち、与えられた記号列を読みながら状態遷移し、その記号列がある言語の文であるかどうかを判定するもの、と定義されている(オートマトン自体は「内部状態と与えられた入力から次の内部状態と出力を決定するもの」で別に形式言語理論に限った話では無いはず。上の定義は形式言語の分野に特化したものだと考えたほうがよさそう)。

上記で定義した正規表現からは機械的に非決定性有限オートマトン(nondeterministic finite automaton, NFA)が生成できる(本書参照)。

決定性有限オートマトン

非決定性有限オートマトンでは与えられた文字列に対し、複数通りの遷移が考えられる場合がある。そうした可能性を除去したものが決定性有限オートマトンである。

ある非決定性有限オートマトンには常に等価な決定性有限オートマトンが存在することが知られており、機械的に求めることができる(本書参照)。

unixのlexはこのような理論に基づいて字句解析のためのプログラムを生成するためのツールである。

疑問

正規言語と文脈自由言語の関係は?
- 正規言語は文脈自由言語の真部分集合
  - 正規表現(そして有限オートマトン)では再帰を表現できないため?

5. 下向き構文解析

上向き構文解析法(bottom up parser)

解析木を下から上に作成していく構文解析法
- 読み込んだ終端記号やすでに還元された非終端記号からなる列がある非終端記号に還元できることがわかったら還元していく
適用できる文法の幅が広い
- 多くのプログラミング言語はLR(k)文法であり、bottom up parserで解析可能
作られる構文解析プログラムが複雑になるため、yaccといったツールを使うことが多い

下向き構文解析法(top down parser)

解析木を上から下に作っていく構文解析法
- これから読み込むものの形を先に仮定してから、それに合致するかどうかを調べていく
構文規則から比較的素直にプログラムが書けるので、手書きのコンパイラに使われることが多い
ただしその解析手法から解析可能な文法は限定されており、適用可能な文法としてLL(k)文法というのが考えられている

擬似的にtop down parserのプログラムを書くと以下のようになる。top down parserでは読み込んだ文字に応じて対応するparser関数を再帰的に呼び出すという感じ。

def expr():
  '''
  Sample code to parse expr.
  expr ::= <term>, { ('+', <term>) | ('-', <term>) }
  '''
  term() # read <term>
  while finish_reading(): # read till the end
    operator() # read '+' or '-'
    term()     # read <term>

TODO

bottom up parser, top down parserで数式計算のためのparserを書いて考えを整理しておきたい
- この場合bottom up parserの方はいわゆる演算子順位文法というのに従うはず
- top down parserの方は左再帰を防ぐための生成規則の書き換えや、First, Followの概念もまとめる

6. 意味解析

意味解析とは、原始プログラムに書いてある名前(識別子)や式や文が何を意味するかについて、構文解析だけではできなかった解析をすることである。

意味解析ではある表に名前、名前の種類(変数、関数、etc.)、型(整数、実数、etc.)、有効範囲(このブロックで有効、etc.)といった情報をまとめることが必要である。そのための表を名前表、記号表、または環境と呼んだりする。この章ではその記号表の作成についてまとめてある。

記号表の構造

記号表は表の探索が効率よく行えるように、一般には配列の形で実装される。
- 各要素(エントリ)が必要とする記憶量が異なることを考慮し、実際はポインタの配列のような形になる。

記号表の探索

記号表に限った話ではないので簡単に。

線形探索
2分法
ハッシュ法

なお作成しているコンパイラでは、記号表の探索は線形で行っている。

ブロック構造と記号表

ブロック構造を持った言語における、名前の有効範囲(scope)の扱い方に関して
内部のブロックへ移る時に記号表の末尾にエントリを足していく
- 探索時は末尾から探すようにすれば、同名のエントリが複数あってもブロック内部のものが使用される
外部のブロックへ戻る時に記号表の末尾インデックスを指すポインタを外部のブロックの末尾のそれへ移すことで、内部のブロックを実質的に削除する

TODO

ハッシュテーブルを車輪にしたい

疑問

記号表はコンパイル時にしか使わない、という認識で正しい?
- 意味解析や目的コードの生成に使用することはあっても、目的コードの実行に必要になるものではないはず
- Pythonの標準ライブラリにはsymtableという記号表を扱うためのAPIが提供されている
  - 「記号表はコンパイラがASTからバイトコードを生成する直前に作られます」

7. 誤りの処理

入力された原始プログラムに誤りが含まれる場合のメッセージや処理に関してまとめてある。

誤りの発見

原始プログラム内のエラーとして主に以下の2つが挙げられている。

構文上のエラー
- 構文解析中に予期せぬtokenが出現したことによるエラー
- e.g. 次に’begin’が来るはずなのに来ていない
意味上のエラー
- 記号表に登録した情報と実際の使い方に矛盾がある場合のエラー
- e.g. 整数として宣言された変数が実数として使用されている

誤りの修復

コンパイラ中にエラーを見つけた際、簡単なものであればどうにかして修復できないか、といった内容がまとめてある。例えば、文の終わりの’;’が無かった場合に補完して処理を続けるといった処理が挙げられている。

ただ個人的にはそういった親切なコンパイラは見たことがないし、またコンパイラの側で勝手に補完、修正するといったことは好ましくないように感じる(警告、提案なら歓迎だけれど)。

正常処理への復帰

原始プログラムにエラーがあるとすれば、一般的には複数のエラーがあると考えるべき。その場合1つのエラーを見つけてすぐに失敗されるよりは最後まで処理を続けてエラーを全て検出してあげた方が親切である。

そのためにはエラーを検出したあとに正常処理へ復帰する必要があり、その方法として以下の2点が挙げられている。

(再帰的下向き構文解析を想定) ある手続きAから呼び出した手続きBが失敗した場合に、手続きBのFollow(後続字句)が出現するまで読みとばす
エラー検出後、その場ではあと処理を行わず、代わりにあるポイントで目的のtokenが出現するまで読みとばすようにすることで対応する
- このようなポイントを同期点と呼ぶ

8. 仮想マシンと通訳系

目的プログラムの生成とその実行に関しての章。

今回作成しているコンパイラでは仮想マシン上での計算を想定しているため、そのための目的コードがどのようなものになるのか、またどのようにして目的コードを生成するのかについてがまとめてある。

仮想マシン

原始プログラムを現実の計算機の機械語に変換するのではなく、その言語に適した仮想的な計算機があると考えて、その仮想機械語に変換する
- コンパイラの作成が簡単になる
仮想マシンとして今まで考えられているものは、後置記法を採用するものがほとんど
- 後置記法で定義された処理はスタックで処理することができる。式の計算にスタックを使用する仮想マシンをスタックマシンと呼ぶ。
  - 例えばJVM
  - Pythonは…と調べてみたが、よくわからなかった
    - というより言語自体に規定されることではないので、処理系によるというのが正解
    - CPythonという一番オーソドックスなものはスタックマシン
  - 今回作成するのもそう
一方で直接レジスタを指定して処理を行う仮想マシンをレジスタマシンと呼ぶ
- 一般的にはこちらの方が処理効率は上がる
- 文脈によってはチューリングマシンという意味で使われることもあるようで注意

仮想マシンの機能

本スタックマシンでは以下の4種類の命令語を用意する。命令語は通常、機能部(何をするか)と操作部(または番地部、何に対してするか)で構成される。

ロード、ストア命令
- 変数、定数からスタックに値を乗せたり、スタックから値を下ろして変数にセットしたりする
演算命令
- スタック先頭の(いくつかの)データを使用して演算を行う。通常演算結果をまたスタックに積む
分岐命令
- 目的コード上の任意の番地へプログラムカウンタを動かす。強制的に移動する(ここではjmp)場合と条件が真の時のみ移動する(ここではjpc)場合がある
呼び出し/戻り命令
- 関数や手続きの呼び出しと戻りを行う

仮想マシンの記憶域管理

本スタックマシンの処理の進み方とスタック領域の使用がどのようになるかについて本節ではまとめてあるが、少し内容が難しかったので実際のコードを元に整理してみることにする。

以下の原始プログラムを用意する。

function plus(x,y)
  var a, b;
begin a := x; b := y;
  return (a + b)
end;

const m = 7, n = 8;
var x;

begin
  write plus(m, n);
  writeln;
end.

コンパイルを行うと以下のような目的コードが得られる。表示の形式は「codes上のindex値: codeの中身」となっている。

ValInst {op_code=OpCode.jmp, value=11}
ValInst {op_code=OpCode.jmp, value=2}
ValInst {op_code=OpCode.ict, value=4}
RefInst {op_code=OpCode.lod, raddr=RelAddr {level=1, addr=-2}}
RefInst {op_code=OpCode.sto, raddr=RelAddr {level=1, addr=2}}
RefInst {op_code=OpCode.lod, raddr=RelAddr {level=1, addr=-1}}
RefInst {op_code=OpCode.sto, raddr=RelAddr {level=1, addr=3}}
RefInst {op_code=OpCode.lod, raddr=RelAddr {level=1, addr=2}}
RefInst {op_code=OpCode.lod, raddr=RelAddr {level=1, addr=3}}
OpInst {op_code=OpCode.opr, op=Operator.add}
RetInst {op_code=OpCode.ret, raddr=RelAddr {level=1, addr=2}}
ValInst {op_code=OpCode.ict, value=3}
ValInst {op_code=OpCode.lit, value=7}
ValInst {op_code=OpCode.lit, value=8}
RefInst {op_code=OpCode.cal, raddr=RelAddr {level=0, addr=2}}
OpInst {op_code=OpCode.opr, op=Operator.wrt}
OpInst {op_code=OpCode.opr, op=Operator.wrl}
RetInst {op_code=OpCode.ret, raddr=RelAddr {level=0, addr=0}}

この目的コードは以下のように実行が進む。ここでpcはプログラムカウンタで実行中のコードのcounter、topは実行中のスタック記憶域の先頭へのindexを表している。

1.  pc=0 , top=0 , code=`ValInst {op_code=OpCode.jmp, value=11}`
  -- pcを11にセット (一番最初に実行される命令は常にmain blockへのjmpとなる)
2.  pc=11, top=0 , code=`ValInst {op_code=OpCode.ict, value=3}`  
  -- topを3つ増加
3.  pc=12, top=3 , code=`ValInst {op_code=OpCode.lit, value=7}`  
  -- stackに7を置く
4.  pc=13, top=4 , code=`ValInst {op_code=OpCode.lit, value=8}`  
  -- stackに8を置く
5.  pc=14, top=5 , code=`RefInst {op_code=OpCode.cal, raddr=RelAddr {level=0, addr=2}}`
  -- `plus`関数呼び出し
6.  pc=2 , top=5 , code=`ValInst {op_code=OpCode.ict, value=4}`  
  -- topを4つ増加
7.  pc=3 , top=9 , code=`RefInst {op_code=OpCode.lod, raddr=RelAddr {level=1, addr=-2}}`
  -- 引数xの値をstackに置く
8.  pc=4 , top=10, code=`RefInst {op_code=OpCode.sto, raddr=RelAddr {level=1, addr=2}}`
  --  変数aへの代入
9.  pc=5 , top=9 , code=`RefInst {op_code=OpCode.lod, raddr=RelAddr {level=1, addr=-1}}`
  -- 引数yの値をstackに置く
10. pc=6 , top=10, code=`RefInst {op_code=OpCode.sto, raddr=RelAddr {level=1, addr=3}}`
  -- 変数bへの代入
11. pc=7 , top=9 , code=`RefInst {op_code=OpCode.lod, raddr=RelAddr {level=1, addr=2}}`
  -- 変数aの値をstackに置く
12. pc=8 , top=10, code=`RefInst {op_code=OpCode.lod, raddr=RelAddr {level=1, addr=3}}`
  -- 変数bの値をstackに置く
13. pc=9 , top=11, code=`OpInst {op_code=OpCode.opr, op=Operator.add}`
  -- stack上位2つを使用して計算
14. pc=10, top=10, code=`RetInst {op_code=OpCode.ret, raddr=RelAddr {level=1, addr=2}}`
  -- `plus`関数からの戻り
15. pc=15, top=4 , code=`OpInst {op_code=OpCode.opr, op=Operator.wrt}`
  -- stack上位1つの出力 (ここでは`plus`の戻り値となる)
16. pc=16, top=3 , code=`OpInst {op_code=OpCode.opr, op=Operator.wrl}`
  -- 改行の出力
17. pc=17, top=3 , code=`RetInst {op_code=OpCode.ret, raddr=RelAddr {level=0, addr=0}}`
  -- programの終了

関数の呼び出し(OpCode.cal)と戻り(OpCode.ret)について更に整理してみる。

関数呼び出し

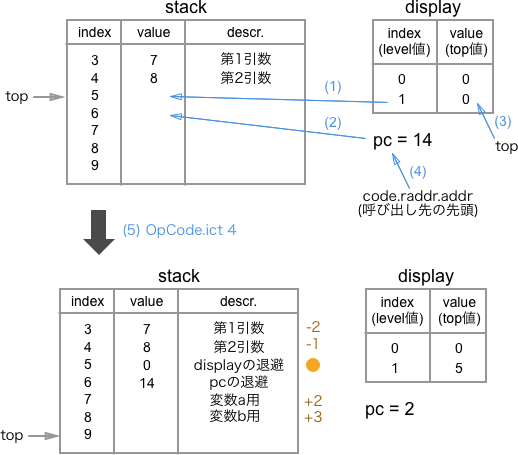
関数呼び出し時は以下のようにstack, display, pcを操作する。

display上の対象関数内部と同一のlevelをstack[top]へ退避する
- displayはlevel(関数の呼び出しの深さ)毎のtopを管理している
- 対象関数名と対象関数内部はlevelが違う。対象関数内部の方が1つ大きい
現在のpc値をstack[top+1]へ退避する
display上の対象関数内部と同一のlevelを現在のtopで更新する
pcを関数呼び出し先のaddressで更新する
topを4つ増加させる (displayの退避、pcの退避、ローカル変数2つ分で計4つ)

この状態から関数内の処理に入るわけで、その際関数に渡した引数や関数内のローカル変数にアクセスするには、displayの対象levelの指すstack上の値(オレンジ丸)からの相対パスで考える。つまりcodeのaddr値としては-2や+2といった値が来るので、それをcodeの持つlevelから求めたdisplay値から足し引きしてstackの該当箇所にアクセスする。

少しわかりにくいけれど、関数の入れ子、再帰的な呼び出しといったことを考えるとこのやり方が都合が良いらしい。

関数の処理が終わると、関数からの復帰処理が始まる。

関数からの復帰

target-code-ret

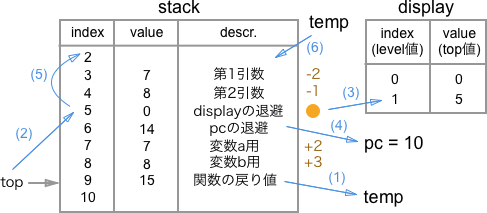
関数からの戻り値(stack[top-1])を一時的に退避する
topをdisplay上の対象関数内部と同一のlevelに保存している値で更新する
- 呼び出し時のものに戻す
退避したdisplayの値を戻す
退避したpcの値を戻す
topを関数に渡した引数の個数分減少させる
一時退避した関数の戻り値をstack[top]に更新する。

topは関数を呼び出している時には基本的に増加するのみで、呼び出し時から減少することはない。関数から戻る際に、もとのtopへ戻してあげれば、実質その関数で使用していたstackを削除したことになる。

ということで、最終的にはtopは関数呼び出し前の値に戻り、stack[top-1]には関数の戻り値が入っているので、次の処理でその値を使用した演算ができる。

読後感

本書を読みPL/0’のコンパイラを作成することでコンパイラに関する概観を掴むことはできた気がします。これから更に深く知りたいなと思う点としては

形式言語理論
オブジェクト指向プログラミング言語におけるクラスがどう扱われているのか
関数型プログラミング言語のコンパイラ

といったところです。

コンパイラ本というと、有名なのはドラゴン本やタイガー本と呼ばれている本のようなので、これらも手が届きそうなら読んでみたいところです。

参考

雑把の仮想マシン(JVM, .NET, BEAM, スクリプト言語, LLVM)
- 各種プログラミング言語の処理系を整理するのに参考になりました。
プログラミング言語処理(佐藤三久教授の講義用資料のよう)
- 本書と同様読みやすくコンパイラに関してまとめてあります。上向き構文解析といった本書ではあまり触れられていない内容もあるので参考になりました。